UM 3D Contact

 Модуль расчета трехмерного контакта (UM 3D Contact)

Общие сведения
Приложения
Немного теории

Общие сведения

Универсальный Механизм 5.0 включает новый модуль UM 3D Contact, который расширяет возможности моделирования контактного взаимодействия. Реализованный метод расчета контакта основан на моделировании взаимодействия произвольных выпуклых многогранников. Поддерживаются следующие геометрические объекты: параллелепипед, цилиндр, конус, сфера, полиэдр.

Для включения контактного взаимодействия пользователю необходимо назначить телам контактные многообразия. Все тела с заданными контактными многообразиями будут взаимодействовать друг с другом. Параметры контактного взаимодействия для каждой пары тел, а также включение/выключение контактного взаимодействия между парами тел настраиваются дополнительно.

Выбранный в качестве контактного многообразия графический образ может не совпадать с графическим образом тела. Упрощенное описание контактного многообразия применяется для снижения вычислительных затрат на обсчет взаимодействия контактных многообразий и, соответственно, для ускорения процесса моделирования, например, для задач моделирования в реальном времени. Кроме того, модель трехмерного контакта поддерживает параметризацию графических объектов, описывающих контактные многообразия, что позволяет рассматривать различную конфигурацию контактирующих тел в достаточно широком диапазоне, просто изменяя соответствующие параметры без необходимости переработки графического образа как такового.

Силовая модель включает упруго-диссипативную компоненту и силу сухого трения, реализующую режимы сцепления и скольжения.

Приложения

Модуль трехмерного контакта существенно расширяет возможности моделирования контактного взаимодействия в Универсальном механизме, а также круг решаемых задач. Несколько коммерческих проектов уже используют модуль трехмерного контакта. Надеемся, что новые реализованные возможности позволят нашим пользователям создавать более адекватные и разнообразные модели.

Пример 1: робототехника

Робототехника - одно из практически значимых приложений модуля. В рамках моделирования динамики колесных и гусеничных роботов в реальном времени учитываются все виды контактных взаимодействий. Моделируется взаимодействие деталей робота, объектов и препятствий на сцене, а также поверхности "земли" сложной формы. Поддерживается манипулирование объектами сцены с помощью схвата манипулятора робота, столкновение элементов конструкции робота с препятствиями на сцене, качение колес робота по сложной поверхности.

Ниже приведены результаты моделирования робота КРТ-200^{1, 2} и его манипулятора:

¹ Модель робота КРТ-200 разработана специалистами Инженерно-технического и учебного центра робототехники (ИТУЦР) госкорпорации "Росатом". Авторы выражают благодарность ИТУЦР и лично Никитину В. Н. за предоставленные материалы.
² Модель робота КРТ-200 с пультом управления включена в демонстрационные примеры, поставляемые с УМ, см. ..samples⁄robots⁄krt_200.

Пример 2: устойчивость античной колонны

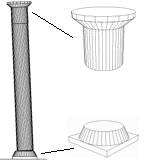Во втором примере рассматривается устойчивость античной колонны при землетрясении^3, 4. Пьедестал колонны установлен на поверхности, движение которой по всем трем направлениям задано в соответствии с замерами, произведенными во время реального землетрясения. Модель состоит из трех тел: пьедестала, колонны и капители. Контактные многообразия всех тел соответствуют их графическим образам.

³ Модель разработана в лаборатории геологии землетрясений универитета Кельна, Германия. Авторы выражают признательность проф. Клаусу Хинцену за предоставленные материалы.
⁴ Модель колонны включена в демонстрационные примеры, поставляемые с УМ, см. ..samples⁄misc⁄earthquake.

Пример 3: фрикционный клин трехэлементной тележки

Еще один пример использования трехмерного контакта - моделирование клиновой системы гашения трехэлементных тележек грузовых вагонов⁵. Все контактные взаимодействия между элементами системы (фрикционный клин, надрессорная балка и боковая рама) реализованы в рамках методологии трехмерного контакта. Для каждого тела сформировано контактное многообразие основанное на графическом образе, импортированном из CAD-системы.

Рассмотренная модель включает только некоторые элементы грузовой трехэлементной тележки и предназначена исключительно для тестирования работы системы фрикционного гашения колебаний и демонстрации возможностей модуля расчета трехмерного контакта. Движение надрессорной балки в модели задано как функция времени с параметризованной амплитудой и частотой.

По следующим ссылкам доступны анимации с результатами моделирования динамики системы:

⁵ Данная модель включена в демонстрационные примеры, поставляемые с УМ, см. ..samples⁄rail vehicles⁄wedgetest3dcontact.

Немного теории

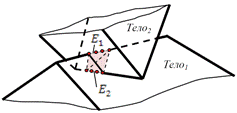
Реализованный метод предназначен для моделирования контактного взаимодействия между двумя выпуклыми полиэдрами. Метод рассматривает взаимодействие между недеформируемыми телами с малыми взаимными внедрениями тел. Метод состоит из двух частей: обнаружение столкновений/взаимопересечений (collision detection) для выпуклых полиэдров и последующий расчет контактных сил. Расчет взаимопересечений использует алгоритм трехмерного отсечения Сайруса-Бека ^{6, 7}. Расчет контактных сил основывается на модели контакта типа «точка-плоскость» и рассчитывается как сумма нормальной упруго-диссипативной силы и касательной силы сухого трения.

Для ускорения вычислительного процесса расчет взаимопересечений разбивается на, так называемый, расчет дальнего и ближнего контакта. Расчет дальнего контакта – это быстрый алгоритм, который выявляет пары тел для дальнейшего, обычно более затратного с точки зрения вычислительных затрат, расчета ближнего контакта. Алгоритм расчета дальнего контакта окружает полиэдры сферами и проверяет пересечение этих сфер на каждом шаге численного интегрирования. Для полиэдров, прошедших через отбор дальнего контакта, выполняется расчет ближнего контакта.

Алгоритм расчета ближнего контакта основан на использовании широко известного в компьютерной графике обобщенного алгоритма трехмерного отсечения Сайруса-Бека, который позволяет определить находится ли некий отрезок полностью или частично внутри выпуклого полиэдра.

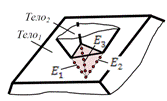
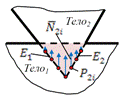
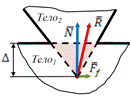
После расчета ближнего контакта необходимо происходит расчет контактных сил. На внедренных ребрах расставляются контактные точки и для них определяются ближайшие грани на втором теле. После чего становится возможным определить контактную силу R которая вычисляется как суперпозиция нормальной упруго-диссипативной силы N и касательной силы сухого трения Ff.

Случаи внедрения типа «Вершина-Грань» и «Ребро-Ребро»	Контактные точки и силы

⁶  M. Cyrus and J. Beck. Generalized Two- and Three-Dimensional Clipping. Computers & Graphics, Vol. 3, pp. 23-28, 1978.
⁷  В некоторых переводах называется алгоритмом Цируса-Бека.